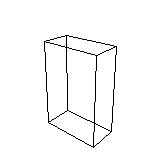
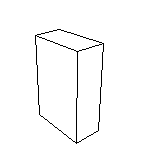
ワイヤフレーム投影によれば,視点からは陰になったり,他の物体に遮られ実際には見えない線も表現されてしまう.実際には隠れて見ることができない線を表現しないようにするための処理が隠線処理(hidden-line removal)である.


表-1 隠線処理の手法
手法 特徴 最大最小法 関数形で示される曲面を表示する場合にのみ用いられる方法.図形を細かく分割して,手前側から描画する方法である.表示開始部分をどこにするかの処理が鍵となる. 法線ベクトル法 ポリゴンの法線ベクトルと視線の内積の正負により隠れ線処理を行う方法である.凸多面体のみに適用可能である. 稜線探索法 任意の多面体の輪郭線をもとに,見える稜線からそれに続く1つ1つの稜線が見えるかどうかを調べていく方法.XYプロッタなどに出力する場合に利用する. 塗り重ね法 スクリーンに遠いポリゴンから描画していくことにより,近いポリゴンが遠くのポリゴンを塗り消していくことを利用した手法. 隠面消去法 レイトレーシング法(光線追跡法)・Zバッファ法・スキャンライン法など画像空間における隠面処理のアルゴリズムがある. (佐藤義雄「実習グラフィックス」アスキー等をもとに作成)ここでは,これらのうち,法線ベクトル法と塗り重ね法を用いた隠線処理について学ぶ.
なお,これらの処理を行うにあたって,ポリゴンのデータを配列に保持する必要がある.理解が容易となるよう(プログラムが読みやすいよう)構造体を用いて,プログラムを改良しているので,リストを参照されたい.
面(ポリゴン)に直交する向きのベクトル(法線)を求め,その角度と視線ベクトルとの角度をもとにして,可視・不可視を判定する方法である.1)法線ベクトルとは..
法線ベクトルは,図-2に示すように,面に直交するベクトルである.図-2 法線ベクトル そのベクトルは,面(すべての点が同一平面上にある)を構成する点のうち,3点の座標値から求めることが可能である.図ー3 ポリゴンの法線
図-3に示すように,点P1,P2,P3,P4からなるポリゴンがあるとする.点は面の表に対して半時計回りに配置されているとすると,その面の表側の法線N のx,y,z成分Nx,Ny,Nzは以下のように表わされる.Nx = (y2-y1)(z3-z2)-(z2-z1)(y3-y2)
Ny = (z2-z1)(x3-x2)-(x2-x1)(z3-z2)
Nz = (x2-x1)(y3-y2)-(y2-y1)(x3-x2)VB上において法線を求める関数は,以下のように書く事ができる.なお,下の関数では大きさ1の単位ベクトルとなるようにしている.
'Point3Dの構造体
Private Type point3D
x As Single
y As Single
z As Single
End Type'ポリゴンの法線を計算するプロシージャ
Private Function calcNormal(p1 As point3D, p2 As point3D, p3 As point3D) As point3D
Dim n As point3D
Dim length As Single
n.x = (p2.y - p1.y) * (p3.z - p2.z) - (p2.z - p1.z) * (p3.y - p2.y)
n.y = (p2.z - p1.z) * (p3.x - p2.x) - (p2.x - p1.x) * (p3.z - p2.z)
n.z = (p2.x - p1.x) * (p3.y - p2.y) - (p2.y - p1.y) * (p3.x - p2.x)
'長さの計算
length = Sqr(n.x ^ 2 + n.y ^ 2 + n.z ^ 2)
'単位ベクトルにする
If length <> 0 Then
calcNormal.x = n.x / length
calcNormal.y = n.y / length
calcNormal.z = n.z / length
End If
End Function
2)可視・不可視の判断
ポリゴンの法線が視点の方向を向いていれば,その面がこちら側を向いていることから,可視ということができる.したがって,平行投影の場合には,法線のNzの向きのみで可視・不可視を判定することが可能である.
中心投影の場合には,図-4に示すように,視点から面に対する視線のベクトルとポリゴンのベクトルとの角度をを求める必要がある.ポリゴンと面との関係が90°未満であれば可視,90°を超えていれば不可視とみなすことができる.
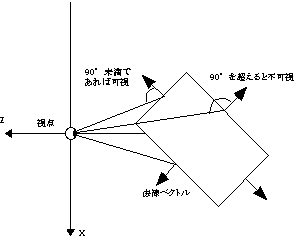
不可視であるか否かは,数学的にはポリゴン上の1点からの視点方向へのベクトル(V)と法線ベクトル(N)との内積の符号で判断される.ただし,Θは2つのベクトルのなす角度である.A = V・N=|V|・|N|cosΘ=VxNx+VyNy+VzNz
3)法線ベクトル法のプログラミング
'ポリゴンの構造体
Private Type Polygon
pnum() As Single ’ポリゴンを構成する点番号
normal As point3D '法線ベクトル
center As point3D '中心座標
zdepth As Single '奥行き
End Type'可視チェックプロシージャ
'視線ベクトルと法線ベクトルの内積により判定
Private Function VisibleCheck(pol As Polygon) As Boolean
Dim length As Single
Dim a As Single
Dim eyeNormal As point3D
length = Sqr(pol.center.x ^ 2 + pol.center.y ^ 2 + pol.center.z ^ 2)
'空間座標から視点方向へのベクトル
'pol.center.x, pol.center.y, pol.center.z はポリゴンの中心座標
If length <> 0 Then
eyeNormal.x = -pol.center.x / length
eyeNormal.y = -pol.center.y / length
eyeNormal.z = -pol.center.z / length
End If
a = eyeNormal.x * pol.normal.x + eyeNormal.y * pol.normal.y + eyeNormal.z * pol.normal.z
If a > 0 Then VisibleCheck = True Else VisibleCheck = False
End FunctionPrivate Sub HiddenDraw(pol As Polygon)
Dim x As Integer
Dim m As Integer
Dim eyeNormal As point3D
Dim length As Single
Dim a As Single
If VisibleCheck(pol) = True Then
For Each x In pol.pnum()
If m = 0 Then
Picture1.PSet (u(pnt(x)), v(pnt(x)))
Else
Picture1.Line -(u(pnt(x)), v(pnt(x)))
End If
m = m + 1
Next
Picture1.Line (u(pol.center), v(pol.center))-Step(u(pol.normal), v(pol.normal))
End If
End Sub
法線ベクトル法では凹多面体や複数の物体が重なり合った場合の隠線処理を行うことができない.一方,重ね塗り法は,凹多面体などでも隠線処理を行うことができる方法である.そのアルゴリズムは隠線処理アルゴリズムの中では比較的簡単である.図-5 塗り重ね法
ここでは,法線ベクトル法と併用することにより,処理の高速化を図っている.
その手順は,以下の通りである.
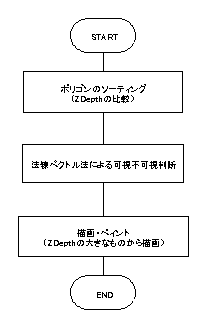
1)ポリゴンのソーティング
法線ベクトル法で求めたポリゴンの中心座標のZ座標は負の値となっているが,これをZDepthすなわち奥行き情報として正の値として扱い,各ポリゴンのZDepthについてソーティングを行う.
プログラムは,以下の通りである.(なお,ソーティングには選択法を用いている.)'ZDepth(奥行き情報)でソーティング
Private Sub ZDepthSort()
Dim zmin As Single
Dim n As Integter
Dim m As Integer
Dim zminpnt As Integer
Dim tmp As Polygon
'ソーティング(選択法)
For n = 0 To polynum - 1
zmin = poly(n).zdepth
For m = n + 1 To polynum - 1
If poly(m).zdepth < zmin Then
zmin = poly(m).zdepth
zminpnt = m
End If
Next
'スワップ
tmp = poly(n)
poly(n) = poly(zminpnt)
poly(zminpnt) = tmp
Next
End Sub2)塗り重ね法+法線ベクトル法
ソーティングした結果,ZDepthの小さいものから大きい順に並んでいる.これについて,ZDepthの大きいものから順に描画していけばよい.なお,描画にあたっては,法線ベクトル法を併用し,描画不要なポリゴンを描画処理から除外するうようにしている.
Private Sub Draw()
Dim n As Integer
Picture1.Cls
'配列のインデックスを1からに変更する.
pnt(0) = setpnt(-1, 1.5, 0.5)
pnt(1) = setpnt(-1, -1.5, 0.5)
・・・・・(略)
rotateY pnt(), 0, 7, rot.y
rotateX pnt(), 0, 7, -eyeR.x
Translate pnt(), 0, 7, -eye.x, -eye.y, -eye.z
polynum = 0 'ポリゴンの数を初期化
MakePoly 0, 1, 2, 3, 0
MakePoly 3, 2, 6, 7, 3
・・・・・・(略)
'ZDepthでソーティング
Call ZDepthSort
'Zdepthの大きなものから描画していく.
For n = polynum - 1 To 0 Step -1
Picture1.ForeColor = QBColor(0)
HiddenDrawPaint poly(n)
Next
End Sub'隠線処理(ペイント)
Private Sub HiddenDrawPaint(pol As Polygon)
Dim x As Variant
Dim m As Integer, n As Integer
Dim disp(100) As UV
Dim pixelfill As UV
Dim wScale As UV
Dim floodctrl As Single
Dim tmpColor As Long
Dim floodflag As Boolean
Dim k As Integer
Dim j As Integer
Dim col As Long
Dim avep As UV
Dim sum As UV
tmpColor = RGB(211, 222, 1) '一時的な描画色(適当な値に設定)
Picture1.ForeColor = QBColor(0) '塗りつぶし色 qbcolor(0)=vbblack
Picture1.FillColor = QBColor(3) '塗りつぶし色 qbcolor(3)=vbgreen
wScale.u = Picture1.Width / Picture1.ScaleWidth
wScale.v = Picture1.Height / Picture1.ScaleHeight
sum.u = 0
sum.v = 0
m = 0
If VisibleCheck(pol) = True Then
For Each x In pol.pnum()
disp(m).u = u(pnt(x)): disp(m).v = v(pnt(x))
If m = 0 Then
Picture1.PSet (disp(m).u, disp(m).v), tmpColor
Else
Picture1.Line -(disp(m).u, disp(m).v), tmpColor
End If
m = m + 1
Next
For n = 0 To m - 2 '閉曲線の場合,始点が2つ含まれるため2を引く
sum.u = disp(n).u + sum.u
sum.v = disp(n).v + sum.v
Next
avep.u = sum.u / (m - 1)
avep.v = sum.v / (m - 1)
pixelfill.u = Int((avep.u - Picture1.ScaleLeft) * wScale.u)
pixelfill.v = Int((avep.v - Picture1.ScaleTop) * wScale.v)
floodflag = True
col = GetPixel(Picture1.hDC, CLng(pixelfill.u) + k, CLng(pixelfill.v) + j)
'塗りつぶし
Picture1.FillStyle = vbFSSolid ' FillStyle プロパティを塗りつぶしに設定します。
Picture1.FillColor = QBColor(3) ' FillColor プロパティを設定します。
FloodFill Picture1.hDC, CLng(pixelfill.u), CLng(pixelfill.v), tmpColor
'描画中心を書かせてみる場合 Picture1.Circle (avep.u, avep.v), 0.01, vbRed
m = 0
For Each x In pol.pnum()
disp(m).u = u(pnt(x)): disp(m).v = v(pnt(x))
If m = 0 Then
Picture1.PSet (disp(m).u, disp(m).v), Picture1.ForeColor
Else
Picture1.Line -(disp(m).u, disp(m).v), Picture1.ForeColor
End If
m = m + 1
Next
End If
End SubPrivate Function VisibleCheck(pol As Polygon) As Boolean Dim length As Single, a As Single Dim eyeNormal As point3D length = Sqr(pol.center.x ^ 2 + pol.center.y ^ 2 + pol.center.z ^ 2) eyeNormal.x = pol.center.x / length eyeNormal.y = pol.center.y / length eyeNormal.z = pol.center.z / length a = eyeNormal.x * pol.normal.x + eyeNormal.y * pol.normal.y + eyeNormal.z * pol.normal.z '本来であれば a < 0 であるが,塗りつぶしのエラーが出ないようにaの範囲を設定する. 'If a < 0 Then VisibleCheck = True Else VisibleCheck = False If a < -0.05 Then VisibleCheck = True Else VisibleCheck = False End Function