１．確率分布

 
確率事象を数学的に表現（近似）

　二項分布
　ポアソン分布
　正規分布　　など

２．母平均の区間推定

　　1)母集団の分散が既知である場合

 
 

問題１ 女子学生200名（母平均157.78cm，母分散25.45(=5.042)）から無作為に抽出した10人の身長が以下のように得られた． 　　　　159cm 158cm,151cm,167cm,151cm,160cm,160cm,158cm,160cm,158cm 母平均の95%信頼区間を推定を行いなさい．ただしz(0.05/2)=1.96とする． 　　　　　　（文献1を一部改変)

　標準正規分布のz(α/2)は，
　    α=.0.01のとき，2.58
　　　α=0.05のとき，1.96
　  　α=0.10のとき，1.64
　エクセルでは，NORMINV(α,平均，分散)で求まる（標準正規分布の場合，平均=0，分散=1）
　　　例)α=0.10のとき，NORMINV(.0.10,0,1)
 

問題２ 以前に作成した統計解析プログラムに，平均の95%信頼区間を求め，表示するようにしなさい．

 

エクセルによる信頼区間の推定 母集団に対する信頼区間を返します。信頼区間とは、標本平均の両側のある範囲のことです。たとえば、通信販売で商品を注文したときに、ある程度の確信を持って、その商品が最も早く到着する日と、最も遅く到着する日を予測することができます。 書式 CONFIDENCE(α, 標準偏差, 標本数) α   信頼度を計算するために使用する有意水準を指定します。信頼度は 100 * (1-α)% で計算されます。つまり、α = 0.05 であるとき、信頼度は 95% になります。 標準偏差,   データ範囲に対する母集団の標準偏差を指定します。これは、既知であると仮定されます。 標本数   標本数を指定します。 解説 ・引数に数値以外の値を指定すると、エラー値 #VALUE! が返されます。 ・α=0 または α=1 である場合、エラー値 #NUM! が返されます。 ・標準偏差,  0 である場合、エラー値 #NUM! が返されます。 ・標本数 に整数以外の値を指定すると、小数点以下が切り捨てられます。 ・標本数 < 1 である場合、エラー値 #NUM! が返されます。 ・α = 0.05 と仮定した場合、標準正規分布曲線より下の領域で、全体の (1-α)% つまり 95% の範囲を計算する必要があります。この値は ±1.96 となります。その結果、信頼区間は次の数式で表されます。 使用例 郊外に住む会社員 50 人を標本として、通勤時間を調査したところ、片道の平均時間が 30 分で、母集団の標準偏差は 2.5 になりました。母集団の平均に対する信頼区間が次の数式で表されるとき、その信頼度は 95% になります。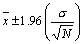 または CONFIDENCE(0.05,2.5,50) = 0.692951 = 30 ± 0.692951 分 = 29.3 〜 30.7 分　　　　　　　　　　　　　　　　　　　　　（Microsoft Excelヘルプより）

 

2)母集団の分散が未知である場合

　母平均μの100(1-α)％信頼区間は下式により表される．
 

エクセルによるtN-1(α/2)の求め方 　エクセルの関数TINVを用いる場合，t分布両側の確率を入力すればよいから，αを2で割る必要はない．すなわち，TINV(α,N-1)とすればよい．例えば標本数5，α=0.05の場合には，=TINV(0.05.4)で求まる．   TINV関数 自由度を指定して、スチューデントの t 分布の逆関数の値を返します。 書式　　TINV(確率, 自由度) 確率   スチューデントの両側 t 分布に従う確率を指定します。 自由度   分布の自由度を指定します。 使用例　　TINV(0.054645,60) = 1.959997   信頼区間の求め方．（95%信頼区間，データはA2からA11に入っていると仮定) 　　1)データの個数の計算しておく．例　A13のセルに　=COUNT(A2:A11) 　　2)データの平均を計算      　 　　　　 A14のセルに　=AVERAGE(A2:A11)     3)標本標準偏差の計算　　　　　　　　A15のセルに =STDEVA(A2:A11)     4)信頼区間（下限）の計算　　　　　　A16のセルに  =A14-TINV(0.05,A13-1)*A15/SQRT(A13)     5)信頼区間（上限）の計算　　　　　　A17のセルに  =A14+TINV(0.05,A13-1)*A15/SQRT(A13)

 
 

問題 1)科学実験においてある溶液のpH値を測定したところ，以下の結果が得られた．母     7.86, 7.89, 7.84, 7.90, 7.82 　　平均の99%の信頼区間を求めなさい． 2)総持寺の境内で捕まえた６匹のアオスジアゲハ夏型の体長は， 　　76mm, 85mm,82mm, 83mm, 76mm, 78mm    であった．アオスジアゲハ夏型の平均体長の90%信頼区間を求めなさい． 3)C市の大きなガソリンスタンドで，乗用車用レギュラーガソリンの平均売上量を求めたい． 　そこで，伝票の中からランダムに８枚抜き出したところ，その値は，以下の通りであった． 45,39,42,57,28,33,40,51  単位はリットル 　このガソリンスタンドを利用している乗用者の平均給油量の95%信頼区間を求めなさい． 文献(1)を一部改変

　　　答　　1)　7.793≦μ≦7.931
　　　　　　 2)   76.8 ≦ μ ≦83.2
              3)　 34.1 ≦ μ ≦ 49.7

３．母比率の区間推定

　母集団がAと非Aの2項母集団を定義づける比率はp：1-pである．この母比率pを区間推定する．

　　母集団からN個の標本をランダムに抽出したとき，この標本の中でAに属する個数がmであれば，
　　　母比率の100(1-α)%信頼区間は，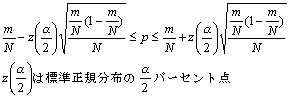

　　ただし，上式は標本数Nが大きい場合(N・m/N≧5　またはN≧30のとき）．

　　

問題 O池におけるブラックバスの生息比率を調査するため，ランダムに178匹の魚類を捕獲したところ，ブラックバスは42匹含まれていた．この池におけるブラックスバス生息比率の90％信頼区間を求めなさい．　　　(文献1)

        (答) 0.184 ≦ p ≦ 0.288

４．標本数の決定　

母集団からの抽出する標本数をどのように定めるか？

1)母比率の区間推定の場合
　母比率の100(1-α)％信頼区間の誤差をＥ以内でおさえたいとき，標本の大きさNは以下の式で与えられる．
　a)母比率pが予想できるとき

　b)母比率pが予想できないとき
 

2)母平均の区間推定の場合
 

問題 1)内閣支持率が0.34と予想されている．この支持率を95%信頼区間で推定したい．このとき誤差を0.02以内に押さえるためには，標本の大きさNをどの程度にすればよいか．ただし，z(0.05/2)=1.96． 2)ひまわりの種子を発芽する確率を標本抽出により区間推定したい．信頼度90％で，誤差を0.05以内におさえるには何粒の種子について発芽実験をすればよいか．ただし，z(1.0/2)=1.64とする． 3)ある製紙会社のトイレットペーパーの紙の長さの標準偏差は今までの経験から約3mであることがわかっている．トイレットペーパーの平均の長さの99%の信頼区間を求めたい．誤差を1m以内にするには，標本の大きさNをどの程度にすればよいか． (文献1を一部改変）

　答)1)2155(人)以上　　　2)269(粒)以上    3)60個