'3次元座標のための構造体
Private Type point3D
    x As Single
    y As Single
    z As Single
End Type
　

１．図形の移動(Translating)

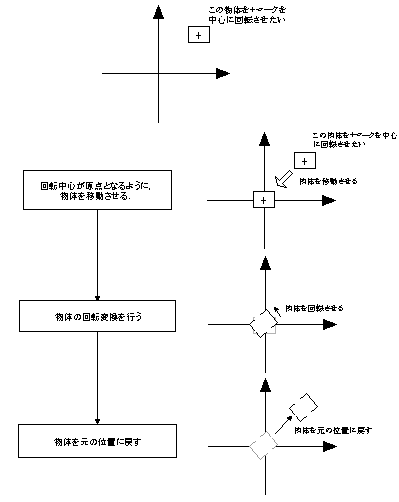
点A(x，y, z)をX方向にtx，Y方向にty，Z方向にtz移動した点A'(X,Y)は，下式によって表現される．

X = x + tx
Y = y + ty
Z = z + tz

図-1　図形の移動（XY平面）  

これをVB上でのサブプロシージャとして定義すれば，以下のようになる．

'図形移動のためのサブプロシージャ
Private Sub Translate(p() As point3D, s As Integer, e As Integer, tx As Single, ty As Single, tz As Single)
    Dim n As Integer
    For n = s To e
        p(n).x = p(n).x + tx
        p(n).y = p(n).y + ty
        p(n).z = p(n).z + tz
    Next
End Sub

    p( ) ： あらかじめ設定された3次元の座標配列が受け渡される．
    s :座標配列のうち，変換を行う開始番号（インデックス）
    e :座標配列のうち，変換を行う終了番号（インデックス）
    tx : X方向の移動量
    ty : Y方向の移動量
    tz : Z方向の移動量
　

２．図形の回転（Rotation)

 ここでZ軸周りに図形を回転すると考える．
図形上の頂点A（x, y, z)をz軸回りにαだけ回転した頂点A'(X,Y,Z)は，下式によって表現される．

    X = x cosα - y sin α
    Y = x sin α + y cos α
    Z = z

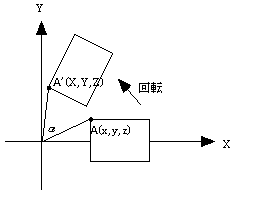図-2 図形の回転（XY平面）  

上式をもとに，Z軸回りに回転変換を行うサブプロージャは，以下のように表わされる．

'Z軸回りの回転変換プロシージャ
Private Sub rotateZ(p() As point3D, s As Integer, e As Integer, rz As Single)
    Dim n As Integer
    Dim x As Single, y As Single, z As Single, rrz As Single

    rrz = rz / 180 * PAI       'sin,cosの計算にラジアンへの変換が必要
    For n = s To e
        x = p(n).x :  y = p(n).y : z = p(n).z         '別の変数に受け渡しておく
                                                                ': は複数の命令を１行に書く場合に使う）
        p(n).x = x * Cos(rrz) - y * Sin(rrz)
        p(n).y = x * Sin(rrz) + y * Cos(rrz)
        p(n).z = z
    Next
End Sub

    p() ： あらかじめ設定された3次元の座標配列が受け渡される．
    s :座標配列のうち，変換を行う開始番号（インデックス）
    e :座標配列のうち，変換を行う終了番号（インデックス）
    rz : Z軸周りの回転角（度）
 

（要注意）      上記プロシージャにおいて，          x = p(n).x :  y = p(n).y : z = p(n).z      というように一度，別の変数に格納しているが，下記のように記載すれば，  　　その手続きが不要になるように思える．  　　　p(n).x = p(n).x*Cos(rrz)-p(n).y*Sin(rrz)            (1)         p(n).y = p(n).x* Sin(rrz) + p(n).y * Cos(rrz)       (2)         p(n).z = z   　しかし，これを計算するとうまく変換できない．  　 それは(2)式でp(n).yの変換を行っているが，この式の中にp(n).xの値を用いている．  　 しかし，(1)式で既にp(n).xは変換済みの値に書き換えられてしまっているため，  　 正しい変換をすることができないためである．

 

同様に，X軸回り，Y軸回りの回転変換も以下のようなプロシージャで可能である．

'X軸まわりの回転変換プロシージャ 　　rxはX軸回りの回転角(度）
Private Sub rotateX(p() As point3D, s As Integer, e As Integer, rx As Single)
    Dim n As Integer
    Dim x As Single, y As Single, z As Single, rrx As Single
    rrx = rx / 180 * PAI
    For n = s To e
        x = p(n).x :  y = p(n).y : z = p(n).z
        p(n).x = x
        p(n).y = y * Cos(rrx) - z * Sin(rrx)
        p(n).z = y * Sin(rrx) + z * Cos(rrx)
    Next
End Sub

'Y軸回りの回転変換プロシージャ 　　rzはZ軸回りの回転角（度）
Private Sub rotateY(p() As point3D, s As Integer, e As Integer, ry As Single)
    Dim n As Integer
    Dim x As Single, y As Single, z As Single, rry As Single
    rry = ry / 180 * PAI
    For n = s To e
        x = p(n).x: y = p(n).y: z = p(n).z
        p(n).x = x * Cos(rry) - z * Sin(rry)
        p(n).y = y
        p(n).z = x * Sin(rry) + z * Cos(rry)
    Next
End Sub

 
（注意）
X軸，Y軸，Z軸回りの変換があるが，これらの変換をどのような順番で行うかによって，最終的な図形の姿勢が異なってくるので，注意すること．

３．任意の点を中心とした図形の回転

 　２．での図形の回転は原点(0,0,0)を中心としたものであった．しかし実際には，物体（オブジェクト）の中心で回転させるなど，任意の点を中心とした回転が必要となる場合が多い．このような変換はどのようにして行うのだろうか．
　物体を任意の中心点においたまま，計算することは非常に厄介なことであり，一般には以下のような方法が取られる.． 図-3　任意の点を中心とした物体の回転

 　つまり，Translate>>Rotate>>Translateという３つの座標変換を行うのである．この方法により，非常に簡単に物体の回転を行うことが可能となる．
 
　

４．図形の拡大と縮小（Scaling）

　図形の拡大，縮小は，図形の各頂点の座標値に対して，その拡大率を乗じてやればよい．
　つまり，図形上の頂点A(x,y)を拡大率sでスケーリング変換するとすれば，その変換後の点A'(X,Y)は，下式により表現される．

X = s・x
Y = s・y
Z = s・z

　これをVB上のサブプロシージャとして定義すれば以下のようになる．

'スケーリング変換を行うサブプロシージャ
Private Sub ScaleA(p() As point3D, s As Integer, e As Integer, sc As Single)
    Dim n As Integer
    For n = s To e
        p(n).x = p(n).x * sc
        p(n).y = p(n).y * sc
        p(n).z = p(n).z * sc
    Next
End Sub

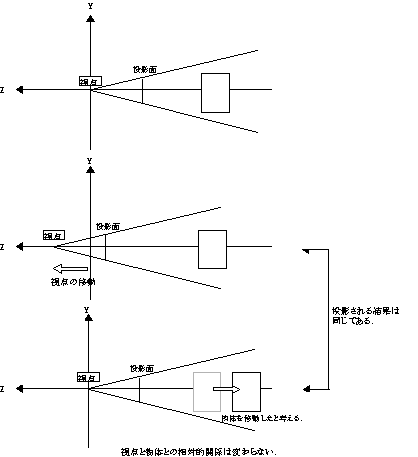
　ただし，原点(0,0,0)に対する拡大率となるので，3.の物体の回転で行なったような図形の移動処理が必要となる場合が多い．
　x, y, zに対する拡大率を個別に設定すれば，任意の方向に対する拡大率を操作できる．

５．視点の移動と回転

 　これまで透視投影変換では視点を常に原点においてその計算を行ってきたが，視点の移動や回転を行う場合に，視点の座標系と物体の座標系を分離する必要があるのでは．．と思うかもしれない．
　しかし，3次元透視投影変換の過程において，視点と物体との座標系とを分離して考えると，その計算が非常に複雑なものとならざるを得ない．そのため，視点座標と物体の座標とを分離することなく，最終的に視点の位置が原点(0,0,0)となるようにして透視投影計算を行うとわかりやすい．
　つまり，視点を移動するのではなく，視点に対して物体を相対的に移動，回転させると考える．（座標変換を段階的に行うとわかりやすい．） 　 図-4　視点移動の考え方